Geneva University

Forensic Authentication Microstructure Optical Set (FAMOS 1)

The forensic authentication microstructure optical set (FAMOS) is a dataset with 5000 unique microstructures from consumer packages for the development, testing and benchmarking of forensic identification and authentication technologies.  All samples have been acquired 3 times with two different cameras giving 30.000 images in total.

The samples have been acquired under industrial conditions, by a system developed by the Stochastic Information Processing (SIP) group and U-NICA, Switzerland.

Example acquisition

Shown here is a single label, acquired twice with both camera's and synchronized. Histogram equilisation has been used for visualization purposes.

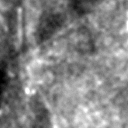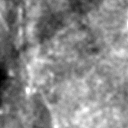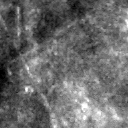cam2_2_hist.png cam2_1_hist.png cam1_2_hist.png cam1_1_hist.png

Acquisition

To acquire a massive set of microstructure images under different conditions, an experimental industrial system was developed. Two color cameras, designated Cam1 and Cam2 respectively, are deployed above a conveyor belt that feeds the paper samples through the system. 

Lighting is identical and consists of a white led ring light together with an angled one approximately 90mm above the surface.

  • Cam1 has a resolution of 2592 x 1944 (5Mp) with a sensor size of 5.7 x4.4 mm and a pixel size of 2.2 micrometer. It has an optical magnification of 1:0.9.
  • Cam2 has a resolution of 1601 x1201 (2Mp), a sensor size of 7 x 5.2mm, a pixel size of 4.4 micrometer and no optical magnification.

Acquired samples are synchronized so that the microstructure always comes from an identical part of the physical sample.  They are then converted to grayscale and stored lossless.

 

PICT0010.JPG

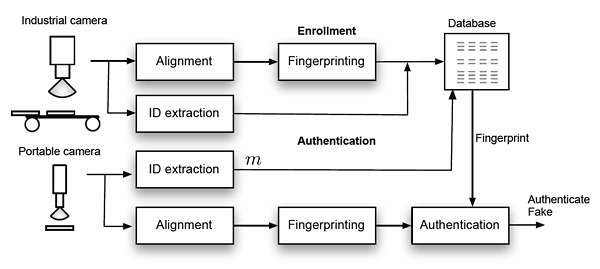
Architecture and Application

The envisioned application architecture is shown below. Samples are enrolled in a factory using a high speed high quality camera. Microstructures are extracted and synchronized. The microstructure, or a fingerprint, are stored with an identifier in a database.

The autentication scenario envisions the use of a cheap portable camera in the field. Again a microstructure is obtained, synchronized and in the case of authentication, presented with an identifier to the architecture.

wifs_architecture_website.png


Dataset layout

The data can be dowloaded as:

  1. Original PNG files, sorted per camera (Camera1 and Camera2) and then per acquisition (A, B, C)
  2. As MATLAB datafiles with one 16384 times 5000 matrix per camera per acquisition.

Terms of Use and Download

Copyright (c), 2012, by the University of Geneva, Stochastic Information Processing group, 7, route de Drize, 1227 Carouge 4, Switzerland.

The user(s) of the FAMOS dataset, herein agree upon the following usage terms and conditions:

  1. The use of the data set is restricted to academic research purpose only. Under these terms, the useage is free.
  2. No redistribution of the dataset is allowed.
  3. If you use this dataset, cite the paper mentioned below and link to this page: http://sip.unige.ch/famos

I Agree

Paper

Please cite FAMOS in academic publications as:

  • S.  Voloshynovskiy, M. Diephuis, F. Beekhof, O. Koval, B. Keel, Towards reproducible results in authentication based on physical non-cloneable functions: the forensic authentication microstructure optical set (FAMOS), Proceedings of IEEE International Workshop on Information Forensics and Security (WIFS), 2012

@INPROCEEDINGS{Diephuis:2012:WIFS,
  author = {Sviatoslav Voloshynovskiy and Maurits Diephuis and Fokko Beekhof and Oleksiy
    Koval and Bruno Keel},
  title = {Towards Reproducible results in authentication based on physical
    non-cloneable functions: The Forensic Authentication Microstructure
    Optical Set (FAMOS)},
  year = {2012},
  address = {Tenerife, Spain},
  month = {December 2--5},
  booktitle = {Proceedings of IEEE International Workshop on Information Forensics
    and Security}
}

Results

If you have interesting results to share with the community, mail us and we will include you on this site!

  • See the WIFS 2012 paper on FAMOS for authentication results for basic cross-correlation and random projections.

Contact Authors